Método de aceitação rejeição - Com exemplo feito em R

O método de aceitação rejeição (ou método de rejeição) é usado para simular valores de uma variável aleatória, geralmente quando o método da inversa não pode ser feito. O método de rejeição consiste no seguinte. Considere uma v.a. com densidade $f(x)$ da qual é necessário gerar valores e $g(x)$ a densidade de outra v.a., da qual é possível gerar valores. No método, é gerado um valor $W$ da v.a. com densidade $g(x)$ e ele é aceito com probabilidade proporcional a $f(W)/g(W)$, com
$$\frac{f(w)}{g(w)} \leq c \text{ para todo $w$.}$$
O algoritmo pode ser escrito como:

1. Gere $W$ com densidade g;
2. Gere um número $U \sim \mathcal{U}(0,1)$;
3. Se $U \leq \frac{f(W)}{c g(W)}$, aceite o valor W. Caso contrário, retorne ao passo 1.

Exemplo no R. 

Suponha que queiramos gerar valores de uma v.a. com densidade

$$f(x) = 12 x^2 (1-x), \ 0 < x < 1.$$

Note que $X\sim B(3,2)$. Como esta variável pertence ao intervalo (0,1), podemos considerar o método com $g(x)=1$, para $x \in (0,1)$, i.e, uma distribuição uniforme. Para determinar o menor valor de $c$ tal que $f(x)/g(x) \leq c$, maximizamos 

$$\frac{f(x)}{g(x)} = 12 x^2 (1-x),$$

obtendo $x=2/3$. Assim, $f(x)/g(x) \leq 12 (2/3)^2 (1/3)=16/9=c$. Assim, temos que 

$$\frac{f(x)}{c \ g(x)} = \frac{27}{4} x^2 (1-x).$$

Assim, para este exemplo o algoritmo fica:

1. Gere $u_1$ e $u_2$ com distribuição $\mathcal{U}(0,1)$;
2. Se $u_2 \leq \frac{27}{4} u^2_1 (1-u_1)$, aceite o valor $u_1$. Caso contrário, retorne ao passo 1.

O código em R, adaptado de uma postagem do blog "Playing with R" (para ler, clique aqui),
pode ser escrito como:

x = runif(10000,0,1) #gerando os valores que podem ser aceitos ou não

accept = c()

for(i in 1:length(x)){

  U = runif(1)

  if(U <= (27/4)*(x[i]^2)*(1-x[i])) {

    accept[i] = 'Yes'

  }

  else if(U > (27/4)*(x[i]^2)*(1-x[i])) {

    accept[i] = 'No'

  }

}  

T = data.frame(x, accept = factor(accept, levels= c('Yes','No')))

xseq=seq(0,1,0.01)

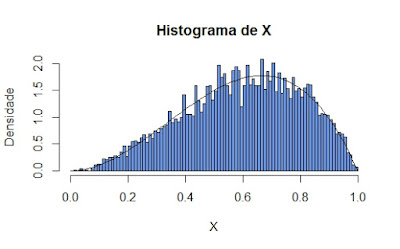
hist(T[,1][T$accept=='Yes'], breaks = seq(0,1,0.01), ylim=c(0,2), freq = FALSE, main = 'Histogram of X', xlab = 'X')

lines(xseq, dbeta(xseq,3,2))  

library(ggplot2)

print(qplot(x, data = T, geom = 'density', color = accept))

print(qplot(x, data = T, geom = 'histogram', fill = accept, binwidth=0.01))